(English | Română)
Grant: Moduli spaces of submanifolds and motion groups
Identifier: PN-III-P4-ID-PCE-2020-2798
Duration: 3 years (2021–2023)
Financed by: UEFISCDI
Contract number: PCE 124/2021
Grant director / Principal Investigator: Martin Palmer-Anghel
Team Members:
|
Abstract
Our domain of research is at the interaction between algebraic topology, quantum topology and algebraic geometry.
The principal objects of study in this project are moduli spaces of submanifolds. These play a central role in algebraic topology, having profound connections with knot theory (predicted by physics) and homotopy theory. In addition, the representation theory of their fundamental groups – motion groups – is very rich.
In dimension 0, these include configuration spaces and braid groups, whose study is a very well-known domain. In higher dimensions, they are more subtle, and their study has developed rapidly recently, leaving nevertheless many open problems.
The aim of our project is to create new interactions between the topology of moduli spaces, TQFTs and motivic and étale cohomology theories, having 4 main directions:
(1) The stable limit of the homology of moduli spaces of disconnected submanifolds. This is an open question for submanifolds of higher dimension.
(2) New kinds of moduli spaces of submanifolds, inspired by physics and number theory. More precisely, the complement of the submanifold is equipped with a 'field' taking values in a bundle.
(3) The definition of new topological representations of motion groups and extensions towards TQFTs. The aim is to create connections with quantum knot invariants.
(4) Algebraic-geometrical analogues of these moduli spaces, and the study of their étale and motivic cohomology.
|
|
|
Results
Our results include the construction of new:
- representations of mapping class groups and motion groups,
- topological models for invariants of knots, links and 3-manifolds,
- algebraic models of homotopy theory,
as well as new theorems about:
- the behaviour of the lower central series of braid groups and their relatives (welded braid groups, surface braid groups, etc.),
- the structure of different freeness-type properties in moduli spaces of line arrangements and of curves in the complex projective plane,
- the homology of non-local configuration spaces and moduli spaces of magnetic monopoles,
- the homology of mapping class groups of infinite-type surfaces.
Expanding a little more on three of these points:
- We give a complete answer — for the family of all (partitioned) surface braid groups, loop braid groups, virtual braid groups and mixed versions of these — to the fundamental but subtle group-theoretical question of whether their lower central series stops. As well as being an important question from the point of view of group theory, the behaviour of these lower central series also controls the possible (higher nilpotent) homological representations that one may construct for these groups.
- We construct explicit topological models for quantum invariants of links and of 3-manifolds. This is expected to open up important avenues of research towards the construction of geometric categorifications of these invariants, as well as the study of their asymptotic behaviour, both of which are key goals in this domain of research.
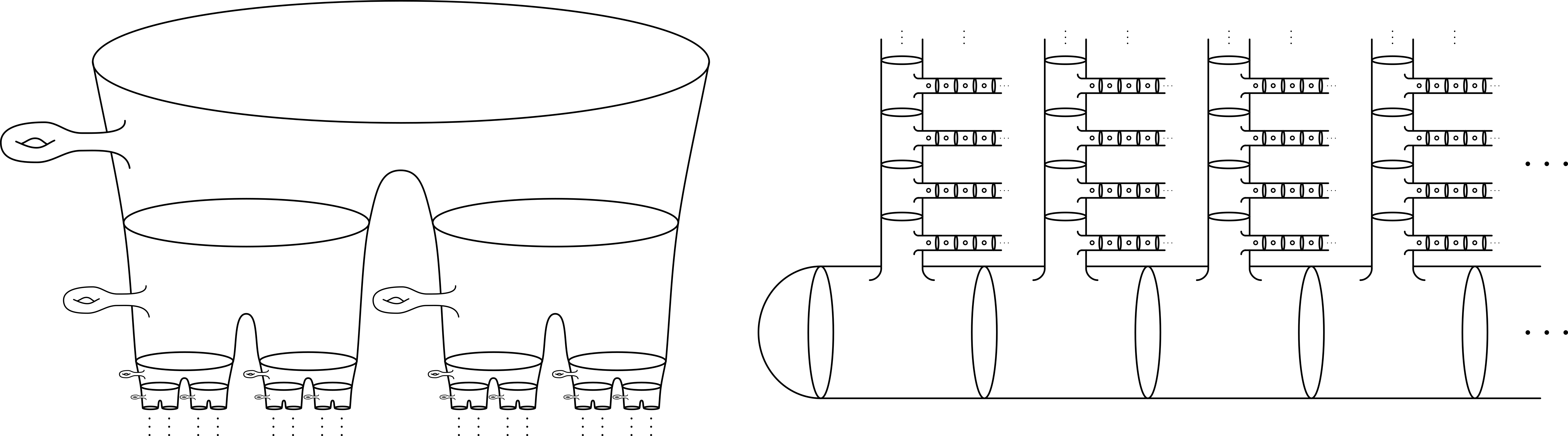
- We prove that there are uncountably many (infinite-type) surfaces S whose mapping class groups Map(S) have trivial homology — an example is illustrated on the left below — and, contrastingly, there are uncountably many surfaces S such that the homology of Map(S) is as "large" as possible: its (integral) homology is uncountable in every positive degree — an example is illustrated on the right below.
|
Publications
- Martin Palmer, Ulrike Tillmann, Configuration-mapping spaces and homology stability
Research in the Mathematical Sciences vol. 8 (2021) no. 38
- Martin Palmer, Arthur Soulié, The Burau representations of loop braid groups
Comptes Rendus. Mathématique vol. 360 (2022) pp. 781-797
- Martin Palmer, Ulrike Tillmann, Point-pushing actions for manifolds with boundary
Groups, Geometry, and Dynamics vol. 16 no. 4 (2022) pp. 1179-1224
- Geoffroy Horel, Martin Palmer, Motivic homological stability of configuration spaces
Bulletin of the London Mathematical Society vol. 55 no. 2 (2023) pp. 892-913
- Cristina Anghel, Quantum knot invariants via the topology of configuration spaces
London Mathematical Society Newsletter vol. 504 (2023) pp. 15-19
- Cristina Anghel, U_q(sl(2))-quantum invariants from an intersection of two Lagrangians in a symmetric power of a surface
Transactions of the American Mathematical Society vol. 376 no. 10 (2023) pp. 7139-7185
- Cristina Anghel, Witten-Reshetikhin-Turaev invariants for 3-manifolds from Lagrangian intersections in configuration spaces
Quantum Topology vol. 14 (2023) pp. 693-731
- Martin Palmer, Ulrike Tillmann, Homology stability for asymptotic monopole moduli spaces
Proceedings of the Royal Society A vol. 479 (2023) Article number: 20230300 (16 pp.)
- Martin Palmer, Xiaolei Wu, Big mapping class groups with uncountable integral homology
Documenta Mathematica vol. 29 no. 1 (2024) pp. 159-189
- Cristina Anghel, ADO invariants directly from partial traces of homological representations
To appear in the New York Journal of Mathematics
Preprint version available at arXiv:2007.15616
- Takuro Abe, Denis Ibadula, Anca Măcinic, On some freeness-type properties for line arrangements
To appear in Annali della Scuola Normale Superiore di Pisa, Classe di Scienze
Preprint version available at arXiv:2101.02150
- Jacques Darné, Martin Palmer, Arthur Soulié, When the lower central series stops: a comprehensive study for braid groups and their relatives
To appear in the Memoirs of the American Mathematical Society
Preprint version available at arXiv:2201.03542
- Cristina Anghel, A globalisation of Jones and Alexander polynomials constructed from a graded intersection of two Lagrangians in a configuration space
To appear in Annales de l'Institut Fourier
Preprint version available at arXiv:2205.07842
- Christian Blanchet, Martin Palmer, Awais Shaukat, Action of subgroups of the mapping class group on Heisenberg homologies
To appear in Contemporary Mathematics
Preprint version available at arXiv:2306.08614
- Martin Palmer, Arthur Soulié, Topological representations of motion groups and mapping class groups – a unified functorial construction
To appear in Annales Henri Lebesgue
Preprint version available at arXiv:1910.13423
Preprints
- Cristina Anghel, Martin Palmer, Lawrence-Bigelow representations, bases and duality
arXiv:2011.02388
- Christian Blanchet, Martin Palmer, Awais Shaukat, Heisenberg homology on surface configurations
arXiv:2109.00515
- Geoffroy Horel, Manuel Krannich, Alexander Kupers, Two remarks on spaces of maps between operads of little cubes
arXiv:2211.00908
- Martin Palmer, Arthur Soulié, The pro-nilpotent Lawrence-Krammer-Bigelow representation
arXiv:2211.01855
- Geoffroy Horel, Binomial rings and homotopy theory
arXiv:2211.02349
- Martin Palmer, Xiaolei Wu, On the homology of big mapping class groups
arXiv:2211.07470
- Anca Măcinic, On torsion freeness for the decomposable Orlik-Solomon algebra
arXiv:2212.12275
- Joana Cirici, Geoffroy Horel, Formality of hypercommutative algebras of Kähler and Calabi-Yau manifolds
arXiv:2302.08492
- Martin Palmer, Arthur Soulié, Polynomiality of surface braid and mapping class group representations
arXiv:2302.08827
- Anca Măcinic, Jean Vallès, A geometric perspective on plus-one generated arrangements of lines
arXiv:2309.10501
- Anca Măcinic, Piotr Pokora, On plus-one generated conic-line arrangements with simple singularities
arXiv:2309.15228
- Anca Măcinic, Piotr Pokora, Addition-deletion results for plus-one generated curves
arXiv:2310.19610
- Cristina Anghel, Universal coloured Alexander invariant from configurations on ovals in the disc
arXiv:2401.17245
- Martin Palmer, Xiaolei Wu, Compact and finite-type support in the homology of big mapping class groups
arXiv:2405.03512
Talks at conferences
- Cristina Palmer-Anghel, "Coloured Jones and Alexander polynomials through Lagrangian intersections in configuration spaces", Homological and quantum invariants, CIRM, Marseille, 8–12 February 2021.
- Geoffroy Horel, "Homotopy theory of operads and the Grothendieck-Teichmüller group", Homotopic and Geometric Galois Theory, Mathematische Forschungsinstitut Oberwolfach, 7–13 March 2021.
- Cristina Palmer-Anghel, "Coloured Jones and Alexander polynomials unified through Lagrangian intersections in configuration spaces", BMC-BAMC: British Mathematical Colloquium, Glasgow, 6–9 April 2021.
- Martin Palmer-Anghel, "Representations of the Torelli group via the Heisenberg group", Workshop for Young Researchers in Mathematics, 20–21 May 2021.
- Geoffroy Horel, "Weight structures and formality" (mini-course of 3 talks), Higher Structures and operadic calculus, CRM, Barcelona, 21–25 June 2021.
- Cristina Palmer-Anghel, "Coloured Jones and Alexander polynomials unified through Lagrangian intersections in configuration spaces", Remote Rendezvous for Quantum Topologists, 9–13 August 2021.
- Cristina Palmer-Anghel, "Coloured Jones and Alexander polynomials unified through Lagrangian intersections in configuration spaces", Perspectives on quantum link homology theories, Regensburg, 9–13 August 2021.
- Martin Palmer-Anghel, "Mapping class group representations via Heisenberg homology", Réunion annuelle du GDR de topologie algébrique, Strasbourg, 26–29 October 2021.
- Cristina Palmer-Anghel, "Coloured Jones and coloured Alexander polynomials unified by a graded Lagrangian intersection", Quantum Field Theories and Quantum Topology Beyond Semisimplicity, Banff International Research Station, Alberta, 1–5 November 2021.
- Cristina Palmer-Anghel, "Uq(sl(2))-invariants quantiques via l'intersection de deux lagrangiennes dans une puissance symétrique d'une surface", Nantes-Orsay seminar on symplectic and contact geometry, Paris-Saclay, 18–19 November 2021.
- Cristina Palmer-Anghel, "Coloured Jones and Alexander polynomials unified through Lagrangian intersections in configuration spaces", Fall Southeastern Sectional Meeting, University of South Alabama, 20–21 November 2021.
- Martin Palmer-Anghel, "Homological stability for asymptotic monopole moduli spaces", Workshop for Young Researchers in Mathematics, IMAR, Bucharest, 19–20 May 2022.
- Martin Palmer-Anghel, "The homology of configuration-section spaces", Twinned Conference on Homotopy Theory with Applications to Arithmetic and Geometry, MPIM Bonn, 27–30 June 2022.
- Cristina Palmer-Anghel, "Coloured Jones and coloured Alexander invariants from two Lagrangians intersected in a symmetric power of a surface", AMS-SMF-EMS Joint International Meeting, Special Session on Low-Dimensional Topology, Grenoble, 18–22 July 2022.
- Geoffroy Horel, "An integral Grothendieck-Teichmüller group", Algebra, Topology and the Grothendieck-Teichmüller group, Les Diablerets, 28 August – 2 September 2022.
- Martin Palmer-Anghel, "Mapping class group representations via Heisenberg, Schrödinger and Stone-von Neumann", Workshop on Cobordisms, Strings, and Thom Spectra, Casa Matemática Oaxaca, 10–14 October 2022.
- Geoffroy Horel, "Binomial rings and homotopy theory", Homotopical Methods in Geometry, Universitat de Barcelona, 9 November 2022.
- Cristina Palmer-Anghel, "A globalisation of the Jones and Alexander polynomials from configurations on arcs and ovals in the punctured disc", Journées de topologie quantique, IMJ-PRG, Paris, 21 November 2022.
- Geoffroy Horel, "An algebro-geometric model for configuration categories", Workshop on Homology of Configuration Spaces, Sorbonne Université, Paris, 15–17 May 2023.
- Anca Măcinic, "Ziegler restrictions and combinatorics of line arrangements", Workshop for Young Researchers in Mathematics, Universitatea Alexandru Ioan Cuza, Iași, 18–19 May 2023.
- Martin Palmer-Anghel, "The homology of big mapping class groups", Workshop for Young Researchers in Mathematics, Universitatea Alexandru Ioan Cuza, Iași, 18–19 May 2023.
- Geoffroy Horel, "Binomial rings and homotopy theory", Generalised Lie algebras in derived geometry, Utrecht University, 29 May – 2 June 2023.
- Geoffroy Horel, "Binomial rings and homotopy theory", Mid-term workshop of the ANR HighAGT, IRMA, Université de Strasbourg, 30 May – 2 June 2023.
- Martin Palmer-Anghel, "Homology of big mapping class groups", Master class: Homology of groups and functors, Université de Lille, 5–9 June 2023.
- Martin Palmer-Anghel, "The homology of big mapping class groups", Homotopy: fruit of the fertile furrow, Isaac Newton Institute, Cambridge, 12–16 June 2023.
- Geoffroy Horel, "Binomial rings and homotopy theory", Homotopy theory in Trondheim, NTNU, Trondheim, 26–30 June 2023.
- Cristina Palmer-Anghel, "Globalising Jones and Alexander polynomials via Lagrangians in configuration spaces", The Tenth Congress of Romanian Mathematicians, Universitatea din Pitești, 30 June – 5 July 2023.
- Martin Palmer-Anghel, "Homological mapping class group representations and lower central series", The Tenth Congress of Romanian Mathematicians, Universitatea din Pitești, 30 June – 5 July 2023.
- Anca Măcinic, "A Yoshinaga-type criterion for POG arrangements", Geometry, Topology and Algebra of Singular Spaces, IMAR, Bucharest, 7–11 July 2023.
- Cristina Palmer-Anghel, "Globalising Jones and Alexander Polynomials (and their quantum generalisations) via configurations in the punctured disc", Mapping class groups: pronilpotent and cohomological approaches, SwissMAP Research Station, Les Diablerets, 18–22 September 2023.
- Geoffroy Horel, "Hypercommutative algebra structures on Kähler and Calabi-Yau manifolds", GDR Théorie de l'Homotopie et Applications, Université de Lille, 24–27 October 2023.
Posters at conferences
- Martin Palmer-Anghel, "On homological stability for configuration-section spaces", BMC-BAMC: British Mathematical Colloquium, Glasgow, 6–9 April 2021 — [link]
- Martin Palmer-Anghel, "On homological stability for configuration-section spaces", Manifolds and K-theory: the legacy of Andrew Ranicki, Edinburgh, 21–25 June 2021 — [link]
Participation in conferences and workshops
(other than those listed further above)
- Anca Măcinic, Logarithmic Vector Fields and Freeness of Divisors and Arrangements: New perspectives and applications, Mathematische Forschungsinstitut Oberwolfach, 24–30 January 2021.
- Martin Palmer-Anghel, Homological and quantum invariants, CIRM, Marseille, 8–12 February 2021.
- Cristina Palmer-Anghel, Workshop for Young Researchers in Mathematics, 20–21 May 2021 (co-organiser).
- Martin Palmer-Anghel, Perspectives on quantum link homology theories, Regensburg, 9–13 August 2021.
- Martin Palmer-Anghel, Workshop: "Cohomology of Arithmetic Groups: Duality, Stability, and Computations", Banff International Research Station, Alberta, 10–15 October 2021.
- Geoffroy Horel, Réunion annuelle du GDR de topologie algébrique, Strasbourg, 26–29 October 2021.
- Martin Palmer-Anghel, Workshop: "Homology and homotopy of configuration spaces", Copenhagen, 15–19 November 2021.
- Martin Palmer-Anghel, Workshop on Polynomial Functors, Topos Institute, 14–18 March 2022.
- Martin Palmer-Anghel, Stability in Topology, Arithmetic and Representation Theory, Purdue University, Indiana, 26–27 March 2022.
- Martin Palmer-Anghel, Braids in Low-Dimensional Topology, ICERM, Brown University, 25–29 April 2022.
- Cristina Palmer-Anghel, Workshop for Young Researchers in Mathematics, IMAR, Bucharest, 19–20 May 2022 (co-organiser).
- Cristina Palmer-Anghel, Quantum Topology and Geometry, Université Paris Cité, 13–17 June 2022.
- Geoffroy Horel, Barcelona Conference on Higher Structures, Universitat de Barcelona, 13–17 June 2022.
- Geoffroy Horel, Twinned Conference on Homotopy Theory with Applications to Arithmetic and Geometry, MPIM Bonn, 27–30 June 2022.
- Geoffroy Horel, Follow-up Workshop to JTP "Topology", Hausdorff Research Institute for Mathematics, Bonn, 5–9 September 2022.
- Martin Palmer-Anghel, Fourth meeting of AlMaRe, Université de Caen, 9–11 January 2023.
- Cristina Palmer-Anghel, Workshop for Young Researchers in Mathematics, Universitatea Alexandru Ioan Cuza, Iași, 18–19 May 2023 (co-organiser).
- Anca Măcinic, The 28th National School on Algebra, Interactions between Algebra and Geometry in Bucharest, University of Bucharest, 24–28 June 2023.
- Cristina Palmer-Anghel, Geometry, Topology and Algebra of Singular Spaces, IMAR, Bucharest, 7–11 July 2023.
- Martin Palmer-Anghel, Geometry, Topology and Algebra of Singular Spaces, IMAR, Bucharest, 7–11 July 2023.
- Martin Palmer-Anghel, Mapping class groups: pronilpotent and cohomological approaches, SwissMAP Research Station, Les Diablerets, 18–22 September 2023.
- Geoffroy Horel, Categories and stacks in algebraic geometry and algebraic topology CATS 7, Centre International de Rencontres Mathématiques (CIRM), Luminy, 16–20 October 2023.
Invited talks at seminars
- Cristina Palmer-Anghel, "Coloured Jones and Alexander polynomials unified through Lagrangian intersections in configuration spaces", Topology Seminar, Stanford, 16 February 2021.
- Cristina Palmer-Anghel, "Coloured Jones and Alexander polynomials unified through Lagrangian intersections in configuration spaces", Séminaire d'algèbre et de géométrie, Caen, 11 May 2021.
- Cristina Palmer-Anghel, "The Witten-Reshetikhin-Turaev invariants for 3-manifolds as state sums of Lagrangian intersections", Knot theory seminar, Warsaw, 28 May 2021.
- Cristina Palmer-Anghel, "Coloured Jones and Alexander polynomials unified through Lagrangian intersections in configuration spaces", Séminaire AGATA, Montpellier, 3 June 2021.
- Cristina Palmer-Anghel, "Uq(sl(2))-quantum invariants for links and 3-manifolds from Lagrangian intersections in configuration spaces", Knots and Representation Theory Seminar, Moscow, 19 July 2021.
- Cristina Palmer-Anghel, "Renormalized Witten-Reshetikhin-Turaev invariants and M-traces associated to the super quantum group Uq(sl(m|n)) at roots of unity", CUNY Representation Theory Seminar, New York, 1 October 2021.
- Martin Palmer-Anghel, "On homological representations of mapping class groups", Algebra/Topology seminar, Copenhagen, 8 October 2021.
- Cristina Palmer-Anghel, "Coloured Jones and Alexander polynomials unified through Lagrangian intersections in configuration spaces", Caltech geometry and topology seminar, Pasadena, 22 October 2021.
- Cristina Palmer-Anghel, "Uq(sl(2))-quantum invariants for links and 3-manifolds from Lagrangian intersections in configuration spaces", Quantum topology seminar, Indiana University Bloomington, 25 October 2021.
- Geoffroy Horel, "Tour de Goodwillie-Weiss algébrique et invariants de nœuds type fini", Séminaire de topologie algébrique, UCLouvain, 16 November 2021.
- Cristina Palmer-Anghel, "Coloured Jones and coloured Alexander invariants from two Lagrangians intersected in a symmetric power of a surface", [K-OS] Knot Online Seminar, CNRS/Paris/Regensburg, 2 December 2021.
- Cristina Palmer-Anghel, "Uq(sl2)-quantum invariants via the intersection of two Lagrangians in a symmetric power of a surface", Séminaire de topologie algébrique, UCLouvain, 7 December 2021.
- Geoffroy Horel, "Finite type knot invariants and the Goodwillie-Weiss tower", Higher algebraic structures in algebra, topology and geometry, Institut Mittag-Leffler, 20 January 2022.
- Cristina Palmer-Anghel, "Coloured Jones and coloured Alexander invariants from two Lagrangians intersected in a symmetric power of a surface", Geometry and Topology seminar, Michigan State University, 8 February 2022.
- Martin Palmer-Anghel, "Mapping class group representations via Heisenberg, Schrödinger and Stone-von Neumann", Fudan Topology Seminar, Shanghai, 10 March 2022.
- Martin Palmer-Anghel, "Mapping class group representations via Heisenberg, Schrödinger and Stone-von Neumann", Topology seminar, New York University, Abu Dhabi, 30 March 2022.
- Cristina Palmer-Anghel, "Uq(sl(2))-invariants quantiques via l'intersection de deux Lagrangiennes dans une puissance symétrique d'une surface", Séminaire de Topologie et Géométrie, Université de Genève, 7 April 2022.
- Geoffroy Horel, "Galois symmetries of knot spaces", Algebraic topology seminar, University of Warwick, 26 April 2022.
- Cristina Palmer-Anghel, "Coloured Jones and coloured Alexander invariants from two Lagrangians intersected in a symmetric power of a surface", Topology seminar, Universität Zürich, 30 May 2022.
- Martin Palmer-Anghel, "Homological stability for asymptotic monopole moduli spaces", Topology seminar, EPFL, Lausanne, 31 May 2022.
- Martin Palmer-Anghel, "Homological representations of motion groups", Geometry and Topology seminar, University of Glasgow, 6 June 2022.
- Cristina Palmer-Anghel, "A globalisation of the Jones and Alexander polynomials from configurations on arcs and ovals in the punctured disc", Topology seminar, Texas State University, 28 October 2022.
- Geoffroy Horel, "Binomial rings and homotopy theory", Topology seminar, EPFL, Lausanne, 28 October 2022.
- Geoffroy Horel, "Binomial rings and homotopy theory", Manifolds, homotopy theory, and related topics, 15 November 2022.
- Geoffroy Horel, "Binomial rings and homotopy theory", Kansas State University Topology Seminar, Kansas, 10 February 2023.
- Geoffroy Horel, "Binomial rings and homotopy theory", Purdue Topology Seminar, Purdue University, Indiana, 15 February 2023.
- Martin Palmer-Anghel, "The homology of big mapping class groups", Séminaire de Topologie et Géométrie, Université de Genève, 9 March 2023.
- Martin Palmer-Anghel, "The homology of big mapping class groups", Group Theory Seminar, ICMAT, Madrid, 14 March 2023.
- Geoffroy Horel, "Configuration categories of surfaces and applications to knot theory", Séminaire d'Homotopie et Géométrie Algébrique, Université de Toulouse, 2 May 2023.
- Cristina Palmer-Anghel, "Globalising Jones and Alexander polynomials via configurations on arcs and ovals in the disc", Geometry and Topology Seminar, Imperial College London, 26 May 2023.
- Geoffroy Horel, "Configuration categories of surfaces and applications to knot theory", Oberseminar Topologie, Universität Münster, 12 July 2023.
- Cristina Palmer-Anghel, "Globalising the Jones and Alexander Polynomials (and their quantum generalisations) via configurations in the punctured disc", Melbourne Topology Seminar, University of Melbourne, 2 October 2023.
- Martin Palmer-Anghel, "The homology of big mapping class groups", Séminaire de topologie, Grenoble, 24 November 2023.
Scientific visits of team members
- Martin Palmer-Anghel, visit to Merton College, Oxford from 14 June to 9 July 2021.
- Martin Palmer-Anghel, visit to the University of Copenhagen from 5 to 8 October 2021.
- Martin Palmer-Anghel, visit to Université de Strasbourg (conference Réunion annuelle du GDR de topologie algébrique) from 25 to 29 October 2021.
- Cristina Palmer-Anghel, visit to the University of South Alabama (online conference Fall Southeastern Sectional Meeting) from 20 to 21 November 2021.
- Martin Palmer-Anghel, visit to Université de Genève from 28 November to 23 December 2021.
- Martin Palmer-Anghel, visit to the American University of Sharjah from 27 March to 2 April 2022.
- Martin Palmer-Anghel, visit to Université de Genève from 8 to 18 May 2022.
- Martin Palmer-Anghel, visit to the University of Glasgow from 6 to 9 June 2022.
- Martin Palmer-Anghel, visit to Université Paris Cité (conference Quantum Topology and Geometry) from 12 to 17 June 2022.
- Martin Palmer-Anghel, visit to MPIM Bonn (conference Twinned Conference on Homotopy Theory with Applications to Arithmetic and Geometry) from 26 to 30 June 2022.
- Martin Palmer-Anghel, visit to Université Grenoble Alpes (conference AMS-SMF-EMS Joint International Meeting) from 17 to 25 July 2022.
- Martin Palmer-Anghel, visit to the University of Oxford (Clay Research Conference and the workshop Physics from the Point of View of Geometry) from 27 September to 1 October 2022.
- Martin Palmer-Anghel, visit to Université de Genève and EPFL from 8 November to 17 December 2022.
- Martin Palmer-Anghel, visit to Université de Caen (conference Fourth meeting of AlMaRe) from 8 to 11 January 2023.
- Cristina Palmer-Anghel, visit to Universitatea din Pitești (conference The Tenth Congress of Romanian Mathematicians) from 30 June to 5 July 2023.
- Martin Palmer-Anghel, visit to Universitatea din Pitești (conference The Tenth Congress of Romanian Mathematicians) from 30 June to 5 July 2023.
- Geoffroy Horel, visit to IMAR from 10 to 16 September 2023.
- Cristina Palmer-Anghel, visit to Les Diablerets (conference Mapping class groups: pronilpotent and cohomological approaches) from 19 to 22 September 2023.
- Martin Palmer-Anghel, visit to Les Diablerets (conference Mapping class groups: pronilpotent and cohomological approaches) from 19 to 22 September 2023.
- Martin Palmer-Anghel, visit to Université de Genève and EPFL from 31 October to 3 December 2023.
Scientific visits (invited guests at IMAR)
- Arthur Soulié (University of Glasgow) from 25 to 30 July 2022.
- Xiaolei Wu (Fudan University, Shanghai) from 6 to 16 September 2023.
- Christine Lescop (Université Grenoble Alpes) from 9 to 16 September 2023.
- Craig Westerland (University of Minnesota) from 9 to 16 September 2023.
|
|
| |
